In the context of SPARQL, queries are patterns that are matched against an RDF graph. Until recently, it was not possible to create a pattern without specifying the exact path of the underlying graph (in terms of real data and/or variables) that would match against the graph. The advent of SPARQL 1.1 introduced property paths as a new graph matching paradigm that allows the employment of Kleene star  * (and it's variant  + ) unary operators to build SPARQL queries that are agnostic of the underlying RDF graph structure. For example, the graph pattern: :Mike (foaf:knows)+ ?person .  is a SPARQL query that asks for all the persons that know somebody that knows somebody (and so on) that :Mike knows.
Property path queries extend the traditional graph pattern matching expressiveness of SPARQL 1.0 with navigational expressiveness.
The ability to express path patterns that are agnostic of the underlying graph structure is certainly a step forward. Still though, it is impossible to retrieve the actual paths through a property path sparql query. In this challenge, we ask for a system capable of returning the actual paths between two URIs in a RDF graph.
Moreover, it is reasonable to assume that a RDF graph contains numerous paths of varying length between two arbitrary nodes. Therefore, another requirement of this challenge is to provide ranked paths according to their length..

Requested system

This challenge evolves around the development and deployment of a system that returns a specific number of ordered paths between two nodes in a given RDF graph. For each one of the Tasks of the Challenge (see the following section), the Challengers should develop a system that makes use of the following information:

1. Start node: The first node of every path that will be returned.
2. End node: The last node of every path that will be returned.
3. k: The required number of paths.
4. ppath expression: A property path expression describing the pattern of the required paths.
5. Dataset: The RDF graph containing the start node and end node.

The system must respond with a set of paths pertaining to the above information. More specifically, each Challenger should provide  k  paths between the Start node and the End node of the Dataset ordered by their length. Such paths should comply to the given ppath expression.
A path is defined as a sequence of nodes and edges within the RDF graph:
(A,P1,U1,P2,U2,P3,U3,..,Un-1,Pn,B)
where A corresponds to the Start node (i.e., subject), B to the End node (i.e., object), Pi to an edge (i.e. predicate) and Ui to an intermediate node. The path length equals to the corresponding number of edges (e.g., the above path length equals to n ).
After developing a system pertaining to the aforementioned requirements, each Challenger should deploy the system in the context of the Tasks below. Essentially, each Task provides a slightly altered set of input data. The next section outlines the Tasks of the Challenge.

Tasks

The Challenge consists of two tasks (see sections below). Both tasks require the implementation of a system capable of returning an ordered set of paths. Such a system should be able to take into consideration the following five input parameters:

1. Start node: The first node of every path that will be returned.
2. End node: The last node of every path that will be returned.
3.  k : The required number of paths.
4. ppath expression: A property path expression describing the pattern of the required paths.
5. Dataset: The RDF graph containing the start node and end node.

A practical example is given for each task (see sections below). Such an example serves as a visual representation of the requirements of each task.

Task1 - part1

The first part of the first task requires a certain number (i.e., k ) of paths between two nodes (i.e. A and  B ) of the evaluation dataset (i.e. RDF graph  D ), ordered by their length. There is no specific pattern such paths should comply to. In SPARQL dialect, such paths should comply to the following property path expression:  !:* .

Practical Example

The image below depicts the example RDF dataset  D1 . Each node is a subject or object while each edge is a predicate.

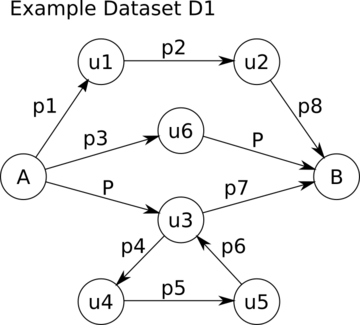
D1 contains exactly 4 paths from  A  to  B :

    1. (A,P,u3,p7,B)
    2. (A,p3,u6,P,B)
    3. (A,p1,u1,p2,u2,p8,B)
    4. (A,P,u3,p4,u4,p5,u5,p6,u3,p7,B)

At this point, it should be mentioned that a path is valid only if it contains unique triples. For example, the path: (A,P,u3,p4,u4,p5,u5,p6,u3,p4,u4,p5,u5,p6,u3,p7,B) is not valid, since the following triple: u3,p4,u4 exists more than once.
If task1 requires 3 paths between A and B within D1, the expected results should be the top-3 shortest paths from A to B:

   1. (A,P,u3,p7,B)
   2. (A,p3,u6,P,B)
   3. (A,p1,u1,p2,u2,p8,B)

Note that the first two paths have the same length, which is equal to 2, since they both contain 2 edges). The third path has a length equal to 3, so it comes after the first two paths.

Task1 - part2
The second part of the first task is meant to test the systems implemented by the challengers in terms of scalability. More specifically, the second part differentiates from the first part by the  k  number of requested paths. This time,  k  is a very large number. Thus, part2 requires a certain number (i.e.,  k ) of paths between two nodes (i.e.  A  and  B ) of the evaluation dataset (i.e. RDF graph  D ), ordered by their length. There is no specific pattern such paths should comply to. In SPARQL dialect, such paths should comply to the following property path expression:  !:* .

Task2 - part1
The first part of the second task differentiates from the corresponding part of the first task by imposing a specific pattern to the required paths. More specifically, the second task requires a certain number (i.e.,  l ) of paths between two nodes (i.e.  A'  and  B' ) of the evaluation dataset (i.e. RDF graph  D ), ordered by their length. Every path should have the edge  P  as the outgoing edge of  A'  , or the incomming edge of  B' . In SPARQL dialect, such paths should comply to the following property path expression: (P/(!:)*)|((!:)*/P) .

Practical Example The image below depicts the example RDF dataset D1. Each node is a subject or object while each edge is a predicate.

If task2 requires 2 paths between A and B within D1, the expected results should be the top-2 shortest paths from A to B that have P as their first or last edge:

1. (A,P,u3,p7,B)
2. (A,p3,u6,P,B)

If task2 requires 3 paths between A and B within D1, the expected results should be the top-3 shortest paths from A to B that have P as their first or last edge:

1. (A,P,u3,p7,B)
2. (A,p3,u6,P,B)
3. (A,P,u3,p4,u4,p5,u5,p6,u3,p7,B)

Note that the path (A,p1,u1,p2,u2,p8,B) is ommitted since  P  is neither the first nor the last edge of the path, so it does not fit to the requirements of the path pattern.

Task2 - part2
The second part of the second task is meant to test the solutions provided by the challengers in terms of scalability. More specifically, the second part differentiates from the first part by the  l  number of requested paths. This time,  l  is a very large number. Thus, task3.2 requires a certain number (i.e.,  l ) of paths between two nodes (i.e.  A'  and  B' ) of the evaluation dataset (i.e. RDF graph  D ), ordered by their length. Every path should have the edge  P  as the outgoing edge of  A'  , or the incomming edge of   B'  . In SPARQL dialect, such paths should comply to the following property path expression:  (P/(!:)*)|((!:)*/P) .

Instructions for Challengers

Challengers should provide both a paper describing their approach and a working system. The working system should be capable of deploying as many of the aforementioned tasks as possible. There are no special requirements for the technological environment of the system. The Challengers may use any infrastructure they see fit (laptpos, PCs, Software as-a-service, etc). More specifically:

• Initially, Challengers have to declare their participation to the Challenge by sending an email to the Organisers (as soon as you are ready!).
• Challengers are able to access the training dataset and the corresponding training material (see section below) so that they can test their implementations.
• A paper must also be submitted until the Challenge papers submission deadline (see the  Important Dates  section: http://2016.eswc-conferences.org/call-challenges). Papers must be submitted in PDF format, following the style of the Springer's Lecture Notes in Computer Science (LNCS) series http://www.springer.com/computer/lncs/lncs+authors, and not exceeding 12 pages in length. All papers will be peer-reviewed. The paper reviewing process will result in the systems that qualify to participate to the event and compete for the highest ranking.
• As soon as the notification to the Challengers is sent, the Organising Committee will make available online the evaluation dataset (Evaluation dataset). Challengers will have a specific time-frame to load the dataset to their system 1.
• The actual input parameters of each task will be published at a specific date (some days after the  Test data (and other participation tools) published  deadline) and the Challengers will have to upload their results for each task within a specific time-frame.
• The Challenge will have its session during the ESWC 2016 Conference. The qualified Challengers will be asked to present their work with a poster and/or laptop.
• The winner of the Challenge as well as the runner-up(s) will be invited to submit a slightly expanded paper as part of the ESWC Satellite Events proceedings (LNCS volume).

Important Notice

Participants with a qualified system must register for the conference and present their system during the Challenge session. A space for demonstration will be allocated for each participant. Participants should bring an A1 poster and/or use their own laptop. The organizers should be contacted in case of any special requirements.

Award

Program Committee

• Sherif Sakr, Senior Researcher in the Software Systems Research Group at National ICT Australia (NICTA), ATP lab, Sydney, Australia
• Emanuele Della Valle, Assistant Professor at the Department of Electronics, Information and Bioengineering of the Politecnico di Milano
• Heiko Paulheim, Assistant Professor at the University of Mannheim, head of Data and Web Science Group
• Dimitrios Tsoumakos, Assistant Professor, Faculty of Informatics and Information Science, Ionian University, member of Computing Systems Laboratory, NTUA
• Guohui Xiao, Assistant professor, Free University of Bozen-Bolzano, member of KRDB Research Centre for Knowledge and Data
• Axel-Cyrille Ngonga Ngomo, Department of Computer Science at the University of Leipzig, member of Semantic Abstraction Group
• Olivier Corby, Researcher at Inria & I3S
• Prof. Dr. Jens Lehmann, Computer Science Institute, University of Bonn, Knowledge Discovery Department, Fraunhofer IAIS

Organizing Committee:

• Ioannis Papadakis, Assistant Professor, Faculty of Informatics and Information Science, Ionian University, member of the organising committee of AImashup Challenge 2013, 2014 - aimashup.org. email: papadakis'at'ionio.gr
• Michalis Stefanidakis, Assistant Professor, Faculty of Informatics and Information Science, Ionian University, member of the organising committee of AImashup Challenge 2014 - aimashup.org. email: mistral'at'ionio.gr
• Phivos Mylonas, Assistant Professor, Faculty of Informatics and Information Science, Ionian University. email: fmylonas'at'ionio.gr
• Brigitte Endres-Niggemeyer, Former professor from Hannover University for Applied Sciences, member of the organising committee of Aimashup Challenge 2010 - 2013. email: brigitteen'at'googlemail.com

Website: https://bitbucket.org/ipapadakis/eswc2016-challenge